向量/矢量¶
约 3551 个字 3 张图片 预计阅读时间 12 分钟
翻译问题
由于一些历史遗留问题,在数学和物理中对于「vector」这一词有不同的翻译。
在物理学科,一般翻译成「矢量」,同时与「标量」一词相对。而在数学学科,一般翻译成「向量」。这种翻译的差别还有「本征」与「特征」、「幺正」与「酉」,等等。
在接下来的叙述中,我们统一使用向量,保证较好的阅读观感。
向量的定义及相关概念¶
向量:既有大小又有方向的量称为向量。一般情况下我们研究的向量为 自由向量,即只要不改变它的大小和方向,起点和终点可以任意平行移动的向量。记作 \(\overrightarrow a\) 或 \(\vec{a}\) 。
有向线段:带有方向的线段称为有向线段。有向线段有三要素:起点,方向,长度,知道了三要素,终点就唯一确定。一般使用有向线段表示向量。
向量的模:有向线段 \(\overrightarrow{AB}\) 的长度称为向量的模,即为这个向量的大小。记为: \(|\overrightarrow{AB}|\) 或 \(|\vec{a}|\) 。
零向量:模为 \(0\) 的向量。零向量的方向任意。记为: \(\overrightarrow 0\) 或 \(\vec{0}\) 。
单位向量:模为 \(1\) 的向量称为该方向上的单位向量。一般记为 \(\overrightarrow e\) 或 \(\vec{e}\) 。
平行向量:方向相同或相反的两个 非零 向量。记作: \(\overrightarrow a\parallel \overrightarrow b\) 。对于多个互相平行的向量,可以任作一条直线与这些向量平行,那么任一组平行向量都可以平移到同一直线上,所以平行向量又叫 共线向量。
相等向量:模相等且方向相同的向量。
相反向量:模相等且方向相反的向量。
向量的夹角:已知两个非零向量 \(\overrightarrow a,\overrightarrow b\) ,作 \(\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b\) ,那么 \(\theta=\angle AOB\) 就是向量 \(\overrightarrow a\) 与向量 \(\overrightarrow b\) 的夹角。记作: \(\langle \overrightarrow a,\overrightarrow b\rangle\) 。显然当 \(\theta=0\) 时两向量同向, \(\theta=\pi\) 时两向量反向, \(\theta=\frac{\pi}{2}\) 时两向量垂直,记作 \(\overrightarrow a\perp \overrightarrow b\) ,并且规定 \(\theta \in [0,\pi]\) 。
注意到平面向量具有方向性,两个向量不能比较大小(但可以比较两向量的模长)。但是两个向量可以相等。
向量的运算¶
向量的加减法¶
在定义了一种量之后,就希望让它具有运算。向量的运算可以类比数的运算,从物理学的角度出发也可以研究向量的运算。
类比物理学中的位移概念,一个人从 \(A\) 经 \(B\) 走到 \(C\),那么他经过的位移为\(\overrightarrow{AB}+\overrightarrow{BC}\),这其实等价于这个人直接从 \(A\) 走到 \(C\),即
上述的公式不要求两向量在同一直线上,即在\(A\)点和\(C\)点固定时,\(B\)点位置的改变并不会影响到最终的和。
通过上述的例子,相信读者不难想到物理中力的合成法则 平行四边形法则 ,其本质即为向量的相加(力即为向量)。由此,我们便可以得到向量的加法法则:
-
向量加法的三角形法则 :若要求和的向量首尾顺次相连,那么这些向量的和为第一个向量的起点指向最后一个向量的终点;
-
向量加法的平行四边形法则 :若要求和的两个向量 共起点,那么它们的和向量为以这两个向量为邻边的平行四边形的对角线,起点为两个向量共有的起点,方向沿平行四边形对角 线方向。
无论是 三角形法则 还是 平行四边形法则 若要求和的两个向量位置不满足上述设定,我们可以通过平移的方式改变位置,平移 自由向量 并不会影响到运算结果。
这样,向量的加法就具有了几何意义。并且可以验证向量的加法满足 交换律与结合律。
因为实数的减法可以写成加上相反数的形式,考虑在向量做减法时也这么写。即:
这样,考虑共起点的向量,按照平行四边形法则做出它们的差,经过平移后可以发现 「共起点向量的差向量」是由「减向量」指向「被减向量」的有向线段。这也是向量减法的几何意义。
常见误区
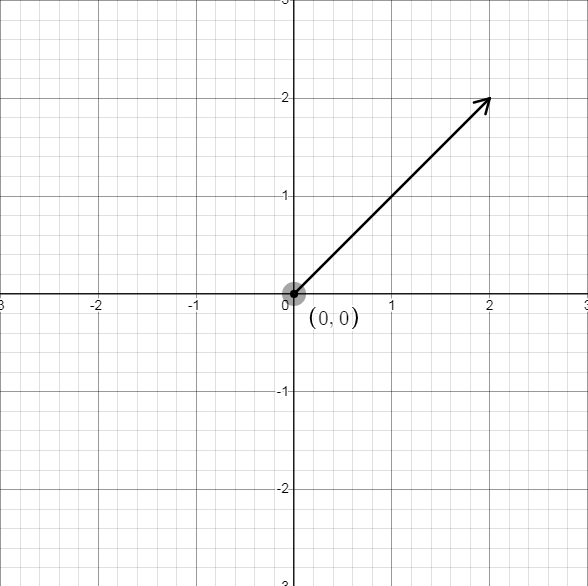
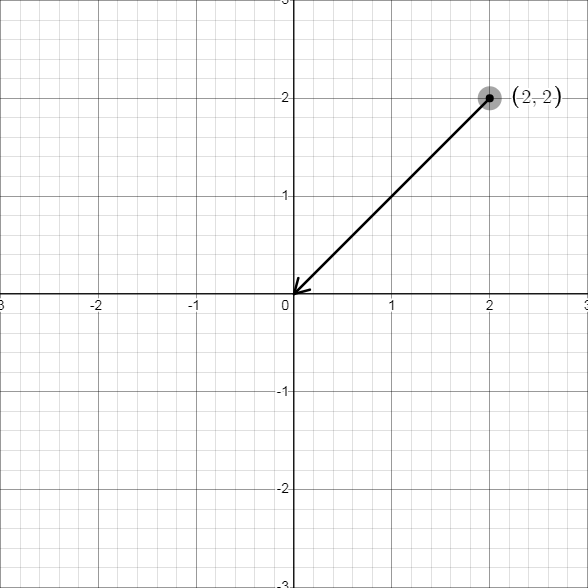
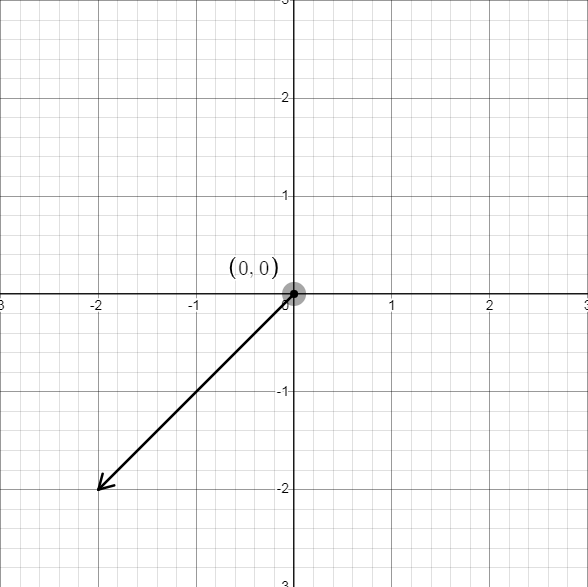
\(-\overrightarrow a\)与\(\overrightarrow a\)的区别在于 方向相反 。但需要注意 方向相反 指的是向量的起点与终点相反,而非只改变终点。具体来说,在下方三张图片中,第一张为原向量,第二张为正确演示。第三张为错误演示。
有时候有两点 A,B,想知道 \(\overrightarrow{AB}\),可以利用减法运算获得:
向量的数乘¶
规定「实数 \(\lambda\) 与向量 \(\overrightarrow a\) 的积」为一个向量,这种运算就是向量的 数乘运算,记作 \(\lambda \overrightarrow a\),它的长度与方向规定如下:
当 \(\lambda >0\) 时,\(\lambda\overrightarrow a\) 与 \(\overrightarrow a\) 同向,当 \(\lambda = 0\) 时,\(\lambda \overrightarrow a=\overrightarrow 0\),当 \(\lambda<0\) 时,\(\lambda \overrightarrow a\) 与 \(\overrightarrow a\) 方向相反。
根据数乘的定义,可以验证有如下运算律:
特别地:
判定两向量共线¶
两个 非零 向量 \(\overrightarrow a\) 与 \(\overrightarrow b\) 共线 \(\iff\) 有唯一实数 \(\lambda\),使得 \(\overrightarrow b=\lambda \overrightarrow a\)。
证明:由数乘的定义可知,对于 非零 向量 \(\overrightarrow a\),如果存在实数 \(\lambda\),使得 \(\overrightarrow b=\lambda \overrightarrow a\),那么 \(\overrightarrow a \parallel \overrightarrow b\)。
反过来,如果 \(\overrightarrow a\parallel \overrightarrow b,\overrightarrow a \not = \overrightarrow 0\),且 \(|\overrightarrow b|=\mu |\overrightarrow a|\),那么当 \(\overrightarrow a\) 与 \(\overrightarrow b\) 同向时,\(\overrightarrow b=\mu \overrightarrow a\),反向时 \(\overrightarrow b=-\mu \overrightarrow a\)。
最后,向量的加,减,数乘统称为向量的线性运算。
翻译问题
由于历史原因,数学学科和物理学科关于「inner product」和「outer product」两个词汇有着五花八门的翻译。
在物理学科,一般翻译成「标积」和「矢积」,表示运算的结果为标量和矢量。高中数学课本上「数量积」和「向量积」也采用了这种意译的办法。
在数学学科,通常也可以翻译成「内积」和「外积」,是两个名词的直译。「点乘」和「叉乘」是根据运算符号得来的俗称,这种俗称也很常见。
在「点乘」运算中,经常省略运算的点符号,在线性代数中更是会直接看作矩阵乘法,不写点符号。
内积/点乘/标积/数量积¶
内积的概念 对于任意维数的向量都适用。
内积有不同但等价的定义方法,下面介绍其中一些。
几何定义 :在 \(n\) 维欧氏空间 \(\mathbf{R}^n\) 下,已知两个向量 \(\overrightarrow a, \overrightarrow b\) ,它们的夹角为 \(\theta\) ,那么:
就是这两个向量的 内积 ,也叫 点积 或 数量积 。其中称 \(|\overrightarrow b|\cos \theta\) 为 \(\overrightarrow b\) 在 \(\overrightarrow a\) 方向上的投影。内积的几何意义即为:内积 \(\overrightarrow a \cdot \overrightarrow b\) 等于 \(\overrightarrow a\) 的模与 \(\overrightarrow b\) 在 \(\overrightarrow a\) 方向上的投影的乘积。
代数定义 :在 \(n\) 维欧氏空间 \(\mathbf{R}^n\) 下,已知两个向量 \(\overrightarrow a = (a_1, a_2, \dots, a_n), \overrightarrow b = (b_1, b_2, \dots, b_n)\) ,那么:
就是这两个向量的 内积 ,也叫 点积 或 数量积。
Danger
内积的几何定义与代数定义在欧氏空间下是等价的,而后者在数学中较为常用,其在计算高多维度向量时更简单。但在物理竞赛中,低维度向量更常见,所以通常使用几何定义进行理解与计算。
在不引起混淆的情况下,内积的点号可以省略不写。如果在向量的右上角有上角标 \(2\) ,表示向量与自身内积的简写,即 向量模长的平方,省略模长记号。该上角标 \(2\) 不可以理解为向量的平方,这是因为,向量内积的结果为标量,不存在除了 \(2\) 以外任何个数的向量的内积。同理,向量模长平方的平方,不可以简写为上角标 \(4\) ,而是必须将上角标 \(2\) 的结果视为一个整体,举个例子:
可以发现,内积得到的结果是一个标量,其特别之处在于,它是关于两个向量分别都线性的双线性运算。具体而言,内积满足:
内积还满足交换律,即:
下面介绍内积运算的一些常见应用。
1.判定两向量垂直:
即互相垂直的两个向量的内积,结果为 \(0\) ;向量与零向量内积,结果为 \(0\) 。如果使用内积为零作为垂直的定义,则可以得出零向量与任何向量都垂直。
2.判定两向量共线:
3.计算向量的模:
4.计算两向量的夹角:
外积/叉乘/矢积/向量积¶
外积有不同但等价的定义方法,下面介绍其中一些。
几何定义:在三维欧氏空间 \(\mathbf{R}^3\) 下,定义向量 \(\overrightarrow a, \overrightarrow b\) 的外积为一个向量,记为 \(\overrightarrow a \times \overrightarrow b\) ,其模与方向定义如下:
-
\(|\overrightarrow a \times \overrightarrow b| = |\overrightarrow a| |\overrightarrow b| \sin \langle \overrightarrow a, \overrightarrow b \rangle\);
-
\(\overrightarrow a \times \overrightarrow b\) 与 \(\overrightarrow a, \overrightarrow b\) 都垂直,且 \(\overrightarrow a, \overrightarrow b, \overrightarrow a \times \overrightarrow b\) 的方向符合右手法则。
注意到外积的模,联想到三角形面积计算公式 \(S=\frac{1}{2}ab\sin C\) ,可以发现外积的几何意义是: \(|\overrightarrow a \times \overrightarrow b|\) 是以 \(\overrightarrow a, \overrightarrow b\) 为邻边的平行四边形的面积。
代数定义:在三维欧氏空间 \(\mathbf{R}^3\) 下,定义向量 \(\overrightarrow a = (x_1, y_1, z_1), \overrightarrow b = (x_2, y_2, z_2)\) 的外积为一个向量 \(\overrightarrow c\) ,记作 \(\overrightarrow c = \overrightarrow a \times \overrightarrow b\) ,其结果可以使用三阶行列式表示:
其中 \(\overrightarrow i, \overrightarrow j, \overrightarrow k\) 表示朝向为坐标轴 \(x, y, z\) 的单位向量,并写在对应坐标处。展开得
下面介绍内积运算的一些常见性质。
外积是关于两个向量分别都线性的双线性运算。具体而言,外积满足:
前两行性质亦可称为分配律,即外积对于向量加法满足乘法分配律。
外积满足反交换律,即:
根据上文内积与外积的几何定义:
可以写出恒等式:
外积满足 Jacobi 恒等式:
下面介绍外积运算的一些常见应用。
1.判定两向量是否共线:
即共线的两个三维向量的外积,结果为 \(\overrightarrow 0\) ;三维向量与自身外积,结果为 \(\overrightarrow 0\) ;三维向量与零向量外积,结果为 \(\overrightarrow 0\) 。若使用外积为零作为两向量共线的定义,则可以得出零向量与任何向量都共线。
2.计算两向量张成的平行四边形面积:
二维向量的情形:对于二维向量,无法计算外积,但是仍然可以计算两向量张成的平行四边形面积:
记 \(\overrightarrow a = (m, n), \overrightarrow b = (p, q)\) ,将平面直角坐标系扩充为空间直角坐标系,原平面位于新坐标系的 \(xOy\) 平面,原本的坐标 \((m, n)\) 和 \((p, q)\) 变为 \((m, n, 0)\) 和 \((p, q, 0)\) 。
那么两个向量的外积为 \((0, 0, mq - np)\) ,因此平行四边形的面积为 \(|mq - np|\) ,可以视为二阶行列式运算结果的绝对值。
此时,根据右手法则和 \(z\) 坐标的符号,可以推断出 \(\overrightarrow b\) 相对于 \(\overrightarrow a\) 的方向,若在逆时针方向则 \(z\) 坐标为正值,反之为负值,简记为 顺负逆正。