圆¶
约 269 个字 3 张图片 预计阅读时间 1 分钟
圆的定义和基本元素¶
-
定义(集合性定义):在平面内,圆是到定点(圆心)距离为定长(半径)的点的集合。
-
符号:通常用\(\odot\)表示圆。
-
基本元素:
- 圆心:圆内一点,到圆上任意点的距离均相等。
- 弦:圆上任意两点间的连线(线段)。
- 圆心角:顶点在圆心的角。
- 圆周角:顶点在圆周上的角。
- 直径:通过圆心的弦,是圆中最长的弦。
- 半径:从圆心到圆上任意一点的线段。
- 弧:圆上任意两点之间的部分,记作\(\mathop{AB}\limits^{\frown}\)。弧根据其对应的圆心角的大小又可以分为优弧(\(>180^\circ\)),半圆(\(=180^\circ\)),劣弧(\(<180^\circ\))。
-
对称性:
- 轴对称:对称轴为直径,有无数条对称轴。
- 中心对称:对称中心为圆心。
- 旋转对称:绕圆心旋转任意角度后,图形与原图形重合。
垂径定理¶
-
原理:圆是轴对称图形。
-
内容:
- 垂直于弦的直径,必然平分该弦。
- 平分弦的直径,必然垂直于该弦。
-
推论:
- 垂径平分弦对应的优弧和劣弧。
- 知二求四(已知以下任意两个条件,可推导出其他四个):
- \(AB\) 为直径
- \(AB \perp CD\)
- \(AB\) 平分 \(CD\)
- \(AB\) 平分 \(CD\) 对应的劣弧
- \(AB\) 平分 \(CD\) 对应的优弧
- \(OB\) 为 \(\angle COD\) 的角平分线
- \(AB\) 为 \(\angle CAD\) 的角平分线
圆心角定理¶
-
内容:
-
在同圆或等圆中,相等的圆心角所对的弦相等。
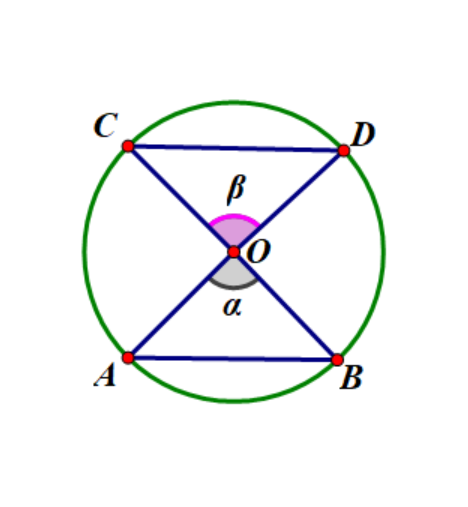
- 例:如图,\(\alpha\) 与 \(\beta\) 互为对顶角(\(AD\) 与 \(BC\) 交于 \(O\)),则 \(\alpha = \beta\),因此 \(AB = CD\)。
-
在同圆或等圆中,圆心角所对的弧长与圆心角成正比:
-
弧度制:弧长 = 圆心角 × 半径(即 $ l = \alpha \cdot r $)。
-
角度制:弧长 = $ \frac{\alpha}{360^\circ} \times \text{周长} $(即 $ l = \frac{\alpha}{360^\circ} \cdot 2\pi r $)。
-
-
圆周角定理¶
-
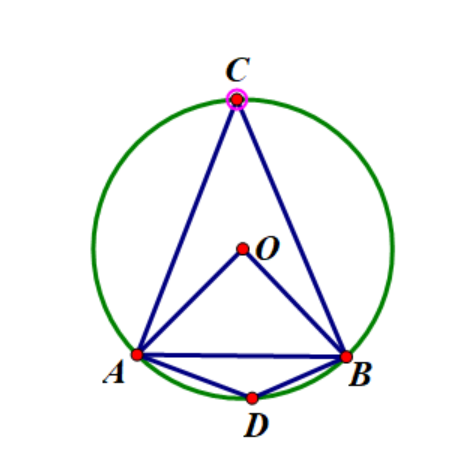
定义:同弧所对的圆周角等于该弧所对圆心角的一半。
- 例:$ \angle ACB = \frac{1}{2} \angle AOB $。
-
互补弧对应圆周角互补:如果两个圆周角对应互补弧,则这两个角互补。
- 例:$ \angle ACB + \angle ADB = 180^\circ $。
-
推论:
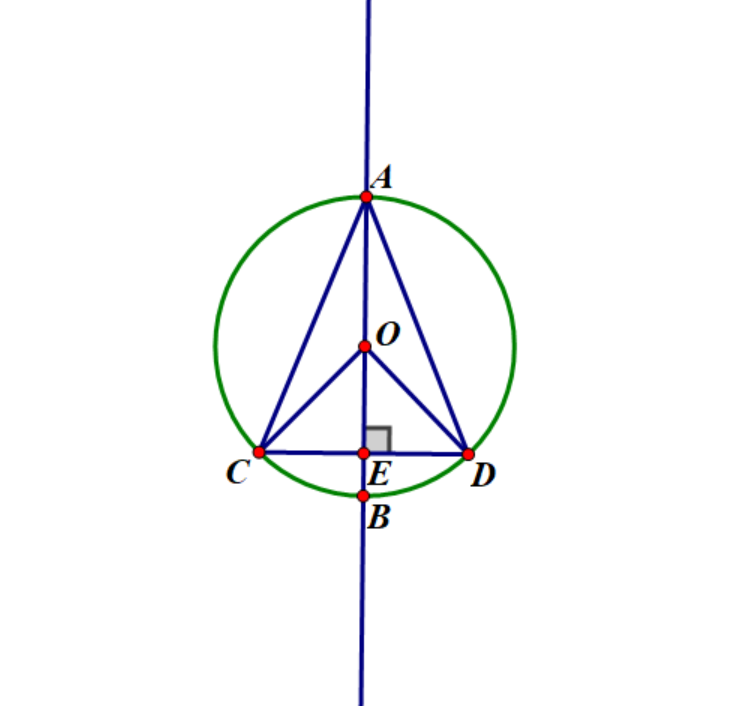
直径所对的圆周角是直角(\(90^\circ\))。
- 例:$ \angle ACB = 90^\circ = \angle ADB $(如图,三角形内接于圆,且 AB 为直径)。
等弧所对的圆周角相等;在等圆中,相等的圆周角所对的弧相等。
- 例:如果 $ \angle C = \angle D $ ,则 \(\mathop{CB}\limits^{\frown} = \mathop{DB}\limits^{\frown}\) 。
等弧所对的弦相等;在等圆中,相等的弧所对的弦相等。
- 例:如果 $ \mathop{AB}\limits^{\frown} = \mathop{CD}\limits^{\frown} $ ,则 \(AB = CD\) 。
圆内接四边形¶
-
定义:四个顶点都在圆上的四边形。
-
性质:
对角互补:圆内接四边形的对角之和为 180°。
- 例: $ \angle BAD + \angle BCD = 180^\circ , \angle ABC + \angle ADC = 180^\circ $。
外角性质:一个角的外角等于其内对角。
- 例:如图,点 \(E\) 在四边形 \(ABCD\) 外,则 $ \angle PAE = \angle C $。
直线与圆的位置关系¶
Info
本节中,记 \(d\) 为 \(\odot O\) 圆心 \(O\) 到直线 \(l\) 的距离,\(r\) 为 \(\odot O\) 的半径。
在平面几何中直线与圆的位置关系有三种,相离,相切,相交。
-
定义:
-
相离:直线与圆没有交点,此时\(d>r\)。
-
相切:直线与圆有且仅有一个交点,相交的点称为切点,过切点的半径垂直于切线,此时\(d=r\)。
-
相交:直线与圆有两个交点,穿过圆的直线称为割线,此时\(d<r\)。
-
-
判定:
-
相离:\(d>r\)。
-
相切:直线与圆交于一点且过此点的半径垂直于直线,或\(d=r\)。
-
相交:\(d<r\)。
-